MUSIQUE

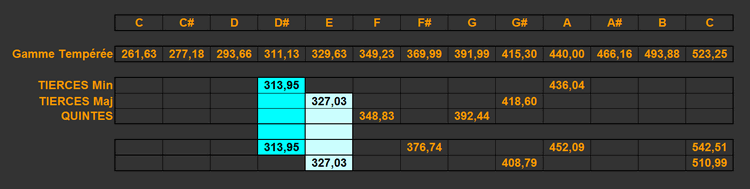
COMMENT CALCULER LES FREQUENCES DES NOTES

L'écart entre la gamme tempérée, les tierces et les quintes

Prenons comme exemple la gamme comprise entre le Do3 et le Do4. Lorsque l'on compare les fréquences de la gamme tempérée comprise entre ces deux notes avec les tierces et les quintes générées à partir de ces deux même notes, il apparaît des divergences.

L'écart entre les tierces et l'octave

Dans l'exemple précédent, si l'on repart des tierces obtenues à partir du Do3, et que l'on ajoute les tierces nécessaires pour arriver au Do4, les valeurs ne correspondent pas à la fréquence du Do4.

Un simple calcul mathématique pourrait nous éclairer:

Les notes des tierces mineures et des tierces majeures sont respectivement reliées à un facteur 1,20 et 1,25.
L'octave représente un facteur 2
Il n'existe pas de combinaison possible de multiplication des facteurs 1,20 et 1,25 pour arriver à 2.

Si nous reprenons la première ligne de notre dernier exemple:

1,2 x 1,2 x 1,2 x 1,2 = 2,07
C D# x D# F# x F# A x F# C

La deuxième ligne de notre dernier exemple donne:

1,25 x 1,25 x1,25 = 1,95
C E x E G# x G# C

 

La spirale des QUINTES du Dr. FICHES

Le Dr. FICHES a proposé une approche vraiment extraordinaire qui permet de définir les fréquences des notes de la gamme.

Pour qu'un son soit harmonieux, il faut que ses différentes composantes présentent une possibilité de "mixage harmonieux de leurs vibrations". Deux notes identiques séparées d'une octave se mélangent très harmonieusement.

En partant de ce principe, le Dr. FICHES a cherché la relation entre les octaves,les quintes et les tierces. Il a observé que lorsqu'à partir d'une note, on enchaîne 12 quintes (12 x 7 demi-tons), on retrouve cette même note 7 octaves au dessus.

C'est mathématique:

• les quintes correspondent à un facteur 1,5 x
• les octaves correspondent à un facteur 2 x

1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 x 1,5 = 2 x 2 x 2 x 2 x 2 x 2 x 2

ou 1,5^12 = 2^7

En enchaînant les quintes en partant du Do1, on trouve:

Sol1, Ré2, La2, Mi3, Si3, Fa#4, Do#5, Sol#5, Ré#6, La#6, Fa7,..... Do8 (7 octaves au dessus de Do1)

En enchaînant 12 quintes, on parcourt donc toute la gamme des notes à travers 8 octaves croissantes.
Le passage d'une octave à l'autre est toujours juste et correspond à un facteur 2. A partir des notes obtenues au moyen du cycle des quintes, il suffit donc de redescendre du nombre d'octaves nécessaires pour retrouver la fréquence de la note désirée.

Dans l'exemple ci dessus, C#1 s'obtient en descendant de 4 octaves la valeur obtenue en c#5;
ou en divisant par 16 la valeur obtenue en C#5 ( 2 x 2 x 2 x 2 = 16)

La gamme de fréquences physiologiques