MUSIQUE !!!!!!! PAGE EN PREPARATION !!!!!!!!!!!!!!

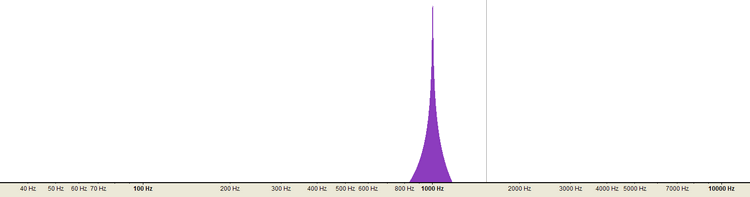
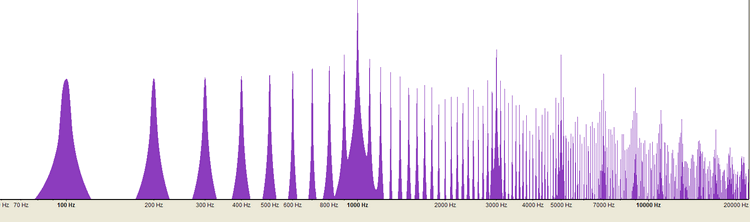
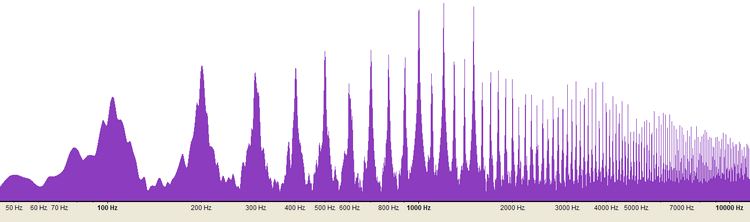
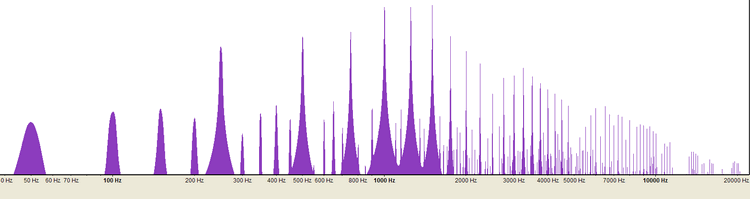
LES HARMONIQUES

Lorsque l'on fait jouer la même note de musique à différents instruments, le son obtenu est très différent: on dit que le timbre est différent.

C'est cette notion de timbre qui nous permettra de différencier et de reconnaître les différents instruments d'un orchestre. En fait, le timbre est très dépendant du nombre et du type d'harmoniques qui sont compris dans le son produit par l'instrument

Prenons un son généré électroniquement à partir d'une onde parfaitement sinusoidale. Si nous analysons le spectre des fréquences qui composent ce son au moyen d'un procédé mathématique (FFT), on obtient 1 seul pic correspondant à la fréquence sinusoïdale du son créé.

exemple de l'analyse FFT d'un son pur sinusoïdal de 1.000 Hz

Si l'on génère un son à partir d'une onde parfaitement carrée et que par un procédé mathématique (FFT), on analyse le spectre des fréquences qui composent ce son, on obtient un pic important correspondant à la fréquence générée mais on obtient aussi toute une série de pics dont les fréquences correspondent aux harmoniques de ce son.

exemple de l'analyse FFT d'un son provenant d'une onde carrée de 1.000 Hz

On retrouve une harmonique inférieure, tous les 1/10 en moins de la fréquence: 900, 800, 700, 600, 500, 400, 300, 200, 100 Hz.
Idem au delà de la fréquence avec des harmoniques plus élevées et plus présentes aux multiples impairs de la fréquence (3 f, 5 f, 7 f,...)

ONDE SINUSOIDALE, HARMONIQUES ET ONDE CARREE

Lorsque l'on génère les harmoniques impaires d'un signal sinusoïdal, la résultante est une onde carrée

Dans cet exemple, la fréquence sinusoïdale est de 5 Hz (courbe jaune). Les trois premières harmoniques impaires sont:
15 Hz (1/3 de la grandeur du signal - en orange); 25 Hz (1/5 de la grandeur - en brun); et 35 Hz (1/7 de la grandeur - en rouge)
La résultante des 4 courbes (fréquence originale + 3 premières harmoniques impaires) apparaît en vert (courbe du bas).
On note que plus on ajoute d'harmoniques impaires, plus on se rapproche d'une onde carrée.

LES ACCORDS ET LES HARMONIQUES

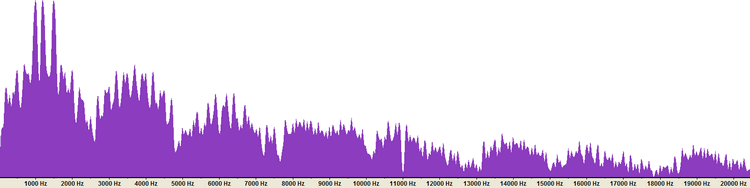
Représentation d'un accord de 1000 Hz mineur (en haut) et majeur (en bas)
Les 3 images représentent un zoom de plus en plus grand (de gauche à droite)

Analyse de l'accord Mineur

Cliquez sur l'image pour l'agrandir
Accord 1000 Hz mineur (1.000 + 1.201,36 + 1.500 Hz) pour une analyse FFT de1.024 points

Sur une échelle linéaire, on retrouve les trois pics (1.000, 1.200 et 1.500 Hz)
Puis plusieurs groupes de pics dont les principaux maximas sont à 3700, 6200.

Cliquez sur l'image pour l'agrandir
Le même accord de1000 Hz mineur pour une analyse FFT d'un plus grand nombre de points (16.000 pts)

On retrouve un très grand nombre d'harmoniques très proches les unes des autres

Cliquez sur l'image pour l'agrandir
Le même accord de1000 Hz mineur pour une analyse FFT Logarithmique de 16.000points

L'analyse logarithmique fait apparaître les fréquences inférieures à l'accord:
900, 800, 700, 600, 500, 400, 300, 200, 100 et 50Hz
A partir de l'accord, on retrouve cette même séquence tous les 100 Hz:
1.000, 1.100, 1.200, 1.300, 1.400...jusque au moins 3.000 Hz.

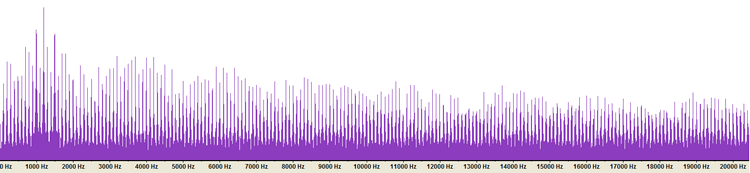
Analyse de l'accord majeur

Cliquez sur l'image pour l'agrandir
Le même accord de1000 Hz majeur (rapport 1 - 1,25 - 1,5) pour une analyse FFT Logarithmique de 16.000points

En dessous de la fréquence, on retrouve 3 gros pics à 750, 500 et 250
on trouve des plus petits pics: 650, 600, 450, 400, 350, 300, 200, 150, 100 et 50

Au dessus de la fréquence, on retrouve des pics tous les 250 jusque 4750HZ: 1750, 2000, 2250,... 4750